Glossary

Poisson Probability

Often one has to compute the probability of getting exactly n occurrences over a period of time or other continuum, for example:

a biologist wants to know if a patient's blood is normal by counting the red corpuscles in the squares of a ruled graticule applied on a slide containing diluted blood;
a quality control professional is asked to accept a batch of electronic components that the supplier guarantees as having at most 233 defectives per million;
an insurance claims officer assesses the likelihood of a home insurance holder having 1 or 2 fires over 5 years;
a highway engineer needs to know the probability of having more than 10 vehicles arriving at a tollgate in 1 minute;
a facilities manager wants to know if 2 switchboard operators can handle 95% of incoming calls;
a design engineer wants to establish the failure rate of a given product with a 95% confidence level;
a hospital manager needs to set up an emergency room knowing that the average rate of arrivals is 1.5 per 1 hour.

The Poisson distribution, named after the 19th century French mathematician Siméon Poisson, applies to such cases as these, where the events take place independently, at a known constant rate derived from a large sample (practically > 50), and with a low probability of occurrence (practically < 10%). The Poisson distribution is discrete, meaning that n can take only certain values, is defined by only 1 parameter (λ or mean), and mean and variance are equal (λ = σ²). For small values of p, Poisson is a good approximation for the binomial distribution.

The solution of the Poisson distribution function is given by the formula :
mathematical solution of the Poisson Probability function

For:
λ = np = mean;
n = random variable;
e = constant equal to approximately 2.718282.

Examples

Check areppim's Poisson Probability Calculator.

Example 1 : Patients arrive at a hospital emergency center at the rate of 3 per hour. What is the probability of two arrivals during the next 30 minutes?

λ = The arrival rate during 30 minutes = (3/60)*30 = 1.5.
n = The random variable = 2 occurrences.

The calculator produces the Poisson probabilities table as follows:

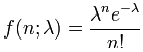
Number of occurrences	Exact Probability	Cumulative Probability
0	0.223	0.223
1	0.335	0.558
2	0.251	0.809

: The probability of exactly 2 arrivals in the next 30 minutes is 25.1%, and the probability of 2 or less arrivals is 80.9%.; Example 2 : Knowing that 3.5% of shoes from the total shop production are rejected, what is the probability of having to reject exactly 4 shoes in a batch of 90 shoes?; λ = The mean rejection rate in a batch of 90 = 90*3.5% = 3.15.
n = The random variable = 4 occurrences.

Number of occurrences	Exact Probability	Cumulative Probability
0	0.043	0.043
1	0.135	0.178
2	0.213	0.390
3	0.223	0.614
4	0.176	0.789

: The probability of having to reject 4 shoes is 17.6%.; Example 3 : The switchboard receives, on average, three telephone calls per minute. What capacity in terms of calls per minute should be installed to cope with incoming calls 95% of the time?; λ = Mean number of calls per minute = 3.
n = The random variable - let us make it 10, in order to explore a wider distribution.

Number of occurrences	Exact Probability	Cumulative Probability
0	0.050	0.050
1	0.149	0.199
2	0.224	0.423
3	0.224	0.647
4	0.168	0.815
5	0.101	0.916
6	0.050	0.966
7	0.022	0.988
8	0.008	0.996
9	0.003	0.999
10	0.001	1.000

: The cumulative Poisson probability indicates that a switchboard of capacity 6 can handle incoming calls 96.6% of the time, i.e. a little better than the targeted 95%.